Chapter 2 — A Gentle Introduction to Static Analysis

21 April 2021

2.2 Abstraction

Example: Semantic Property of Interest: Reachability

Realistic application for C programs:

where it dereference a null pointer
where it writes over a dangling pointer

Definition: Abstraction

We call abstraction a set 𝒜 of logical properties of program states, which are called abstract properties or abstract elements. A set of abstract properties is called an abstract domain.

Definition: Concretization

Given an abstract element

a

of 𝒜, we call concretization the set of program states that satisfy it. We denote it by

\gamma(a)

Abstraction is not unique – some abstractions yield simpler computer representations and less costly algorithms than others:

Definition: Best Abstraction

We say that $a$ is the best abstraction of the concrete set $S$ if and only if

$S \in \gamma(a)$ , and
for any $a^{\prime}$ that is an abstraction of $S$ (i.e., $S \in \gamma(a^{\prime})$ ), then $a^{\prime}$ is a coarser abstraction than $a$

If $S$ has a best abstraction, then the best abstraction is unique. When it is defined, we let α denote the function that maps any concrete set of states into the best abstraction of that set of states.

The best abstraction may not be available. But the impossibility to define or compute the best abstraction is in no way a serious flow for the analysis, as it just lead to conservative but sound results.

Think of the "reachability" semantic property of a program that acts on 2D space:

abstraction	idea
intervals abstraction	the abstract elements of the interval abstract are defined by constraints of the form $l_{\rm{X}} ≤ \rm{X}, \rm{X} ≤ h_{\rm{X}}, l_{\rm{Y}} ≤ \rm{Y}, \rm{Y} ≤ h_{\rm{Y}}$	always has the best abstraction non-relational simpler, more efficient representation
convex polyhedra abstraction	the abstract elements of the convex polyhedra abstract domain are conjunctions of linear inequality constraints, e.g. $\rm{X} - \rm{Y} ≥ -0.5$ $\rm{X} ≤ 2.5$	may not have the best abstraction relational more expressive, but more complex and less efficient

abstraction

idea

intervals abstraction

the abstract elements of the interval abstract are defined by constraints of the form $l_{\rm{X}} ≤ \rm{X}, \rm{X} ≤ h_{\rm{X}}, l_{\rm{Y}} ≤ \rm{Y}, \rm{Y} ≤ h_{\rm{Y}}$

always has the best abstraction
non-relational
simpler, more efficient representation

convex polyhedra abstraction

the abstract elements of the convex polyhedra abstract domain are conjunctions of linear inequality constraints, e.g.

$\rm{X} - \rm{Y} ≥ -0.5$
$\rm{X} ≤ 2.5$

may not have the best abstraction
relational
more expressive, but more complex and less efficient

2.3 A Computable Abstract Semantics: Compositional Style

A compositional approach to static analysis: to analyze a sequence of commands, "composes" the analyses of each sub-command

2.3.1 Abstraction of Initialization

2.3.2 Abstraction of Post-Conditions

abstract pre-condition: an abstraction of the states that can be observed before a program fragment
abstract post-condition: an abstraction of the states that can be observed after that program fragment
transfer function: an abstract operation that accounts for the effect of a basic program statement

Definition: Sound analysis by abstract interpretation in compositional style

We consider a static analysis function analysis that inputs a program and an abstract pre-condition and returns an abstract post-condition. We say that analysis is sound if and only if the following condition holds:

If an execution of p from a state (x, y) generates that state (x′, y′),
then for all abstract element

a

such that (x, y) ∈ γ(

a

),
(x′, y′) ∈ γ(analysis(p,

a

))

The definition above entails that:

the analysis will produce sound results in the sense of the soundness definition when considering the property 𝒫 of interest. Since the analysis over-approximates the states the program may reach, if it claims that 𝒫 is not reachable, then we are sure that the program cannot reach 𝒫.
the analysis is not complete in the sense of the soundness definition, since it accepts analyses that produce coarse over-approximations

2.3.3 Abstraction of Non-Deterministic Choice

Abstract interpretation will produce an over-approximation of both cases, as the union of two sets of abstract elements.

Note

This is another reason for the incompleteness of the analysis: it cannot express precise disjunctive properties (the several solutions will be presented in section 5.1).

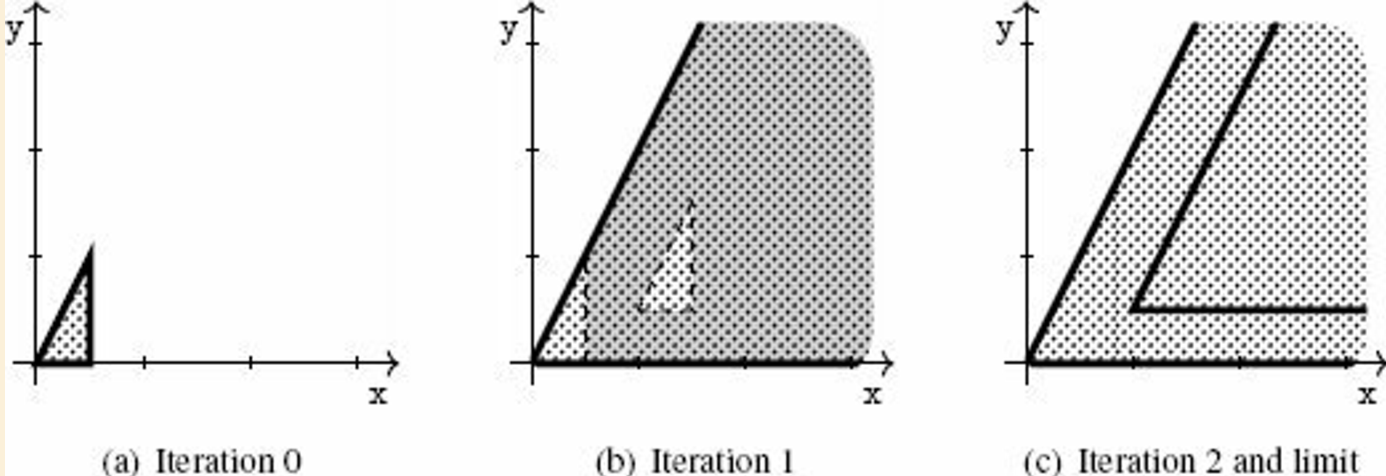
2.3.4 Abstraction of Non-Deterministic Iteration

An interesting fact about static analysis

No analysis can ensure that an iteration will terminate with the abstract post-condition (even if computed), because the halting problem cannot be computed exactly in finite time.

setup:
- program p consists of a loop with body b: p $::=$ iter{ b }
- $\texttt{b}_k$ : program that iterates b $k$ times
- $\texttt{p}_k$ : program that iterates b at most $k$ times
  - implies: $\texttt{p}_{k+1}$ is equivalent to $\texttt{p}_k$ or $\{\texttt{p}_k; \texttt{b}\}$
idea: recursively applies analysis
- $\texttt{analysis}(\texttt{p}_{k+1}, a) = \texttt{union}(\texttt{analysis}(\texttt{p}_k, a), \texttt{analysis}(\texttt{b}, \texttt{analysis}(\texttt{p}_k, a)))$
- $\texttt{R} \leftarrow \texttt{union}(\texttt{R}, \texttt{analysis}(\texttt{b}, \texttt{R}))$
- analysis converges if R stabilizes
approach: force the number of abstract elements to decrease over iteration
- widening: over-approximates unions, enforces convergence
  - $\texttt{widen}(a_0, a_1)$ :
    - keeps all constraints of $a_0$ that are also satisfied in $a_1$ and
    - discards all constraints of $a_0$ that are not satisfied in $a_1$ (hence to subsume $a_1$ )
- inclusion: inputs abstract elements $a_0, a_1$ and returns true only when it can prove that $γ(a_0) ⊆ γ(a_1)$

Algorithm: $\texttt{analysis(iter\{p\}}, a)$

R ← a;
repeat
    T ← R;
    R ← widen(R, analysis(p, R));
until inclusion(R, T)
return T;

Note

Widening is another source of potential incompleteness, but fortunately there are many techniques to make the analysis of loops more precise.

Example: Loop unrolling

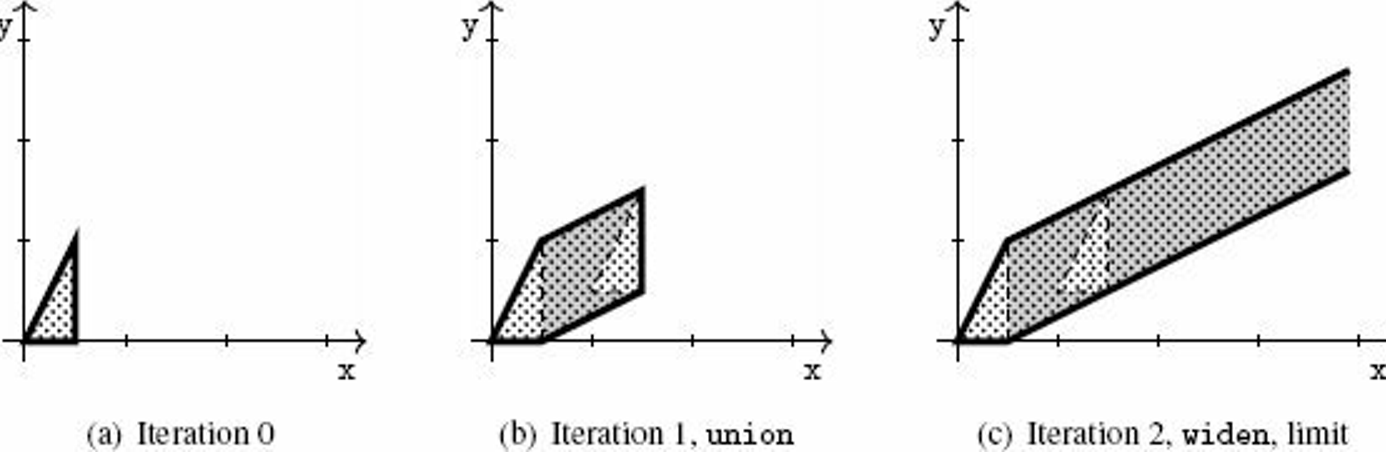
To unroll the first iteration of the loop into the union of {{}; b} can ease the effect of the succeeding widenings.

	program that acts on 2D space	abstract iteration
original	`init({(x,y) \| 0 ≤ y ≤ 2x and x ≤ 0.5}) iter{ translation(1, 0.5) }`
loop unrolled	`init({(x,y) \| 0 ≤ y ≤ 2x and x ≤ 0.5}) {} or { translation(1, 0.5) } iter{ translation(1, 0.5) }`

program that acts on 2D space

abstract iteration

original

init({(x,y) | 0 ≤ y ≤ 2x and x ≤ 0.5})
iter{
  translation(1, 0.5)
}

abstract-iteration

loop unrolled

init({(x,y) | 0 ≤ y ≤ 2x and x ≤ 0.5})
{} or {
  translation(1, 0.5)
}
iter{
  translation(1, 0.5)
}

abstract-iteration-loop-unrolled

2.3.5 Verification of the Property of Interest

The analysis discussed so far actually computes as intermediate results over-approximations for all the interesting states of the input program, and thus we can just monitor them and use it for the verification of the property of interest.

2.4 A Computable Abstract Semantics: Transitional Style

Idea: compute, from the outset, all occurring intermediate states

2.4.1 Semantics as State Transitions

The goal of the analysis: to collect all the states occurring in all possible transition sequences of the input program.

program: a collection of statements with a well defined execution order
program counter (program point): a unique label assigned to each statement of the program
control flow: the execution order, specified by a relation between the labels (from current program points to next program points)

The algorithm works very similarly to the "compositional style", but it will compute states per statement and iterates until all the statement states get converged.

2.5 Core Principles of a Static Analysis

The three-stage approach for static analysis:

selection of the semantics and properties of interest
choice of the abstraction
derivation of the analysis algorithms from the semantics and from the abstraction