2.2 Abstraction
Realistic application for C programs:
where it dereference a null pointer
where it writes over a dangling pointer
Abstraction is not unique – some abstractions yield simpler computer representations and less costly algorithms than others:
We say that is the best abstraction of the concrete set if and only if
, and
for any that is an abstraction of (i.e., ), then is a coarser abstraction than
If has a best abstraction, then the best abstraction is unique. When it is defined, we let α denote the function that maps any concrete set of states into the best abstraction of that set of states.
The best abstraction may not be available. But the impossibility to define or compute the best abstraction is in no way a serious flow for the analysis, as it just lead to conservative but sound results.
Think of the "reachability" semantic property of a program that acts on 2D space:
abstraction | idea | |
|---|---|---|
intervals abstraction | the abstract elements of the interval abstract are defined by constraints of the form |
|
convex polyhedra abstraction | the abstract elements of the convex polyhedra abstract domain are conjunctions of linear inequality constraints, e.g. |
|
2.3 A Computable Abstract Semantics: Compositional Style
A compositional approach to static analysis: to analyze a sequence of commands, "composes" the analyses of each sub-command
2.3.1 Abstraction of Initialization
2.3.2 Abstraction of Post-Conditions
abstract pre-condition: an abstraction of the states that can be observed before a program fragment
abstract post-condition: an abstraction of the states that can be observed after that program fragment
transfer function: an abstract operation that accounts for the effect of a basic program statement
analysis that inputs a program and an abstract pre-condition and returns an abstract post-condition. We say that analysis is sound if and only if the following condition holds: p from a state (x, y) generates that state (x′, y′),then for all abstract element such that (
x, y) ∈ γ(),(
x′, y′) ∈ γ(analysis(p, ))The definition above entails that:
the analysis will produce sound results in the sense of the soundness definition when considering the property 𝒫 of interest. Since the analysis over-approximates the states the program may reach, if it claims that 𝒫 is not reachable, then we are sure that the program cannot reach 𝒫.
the analysis is not complete in the sense of the soundness definition, since it accepts analyses that produce coarse over-approximations
2.3.3 Abstraction of Non-Deterministic Choice
Abstract interpretation will produce an over-approximation of both cases, as the union of two sets of abstract elements.
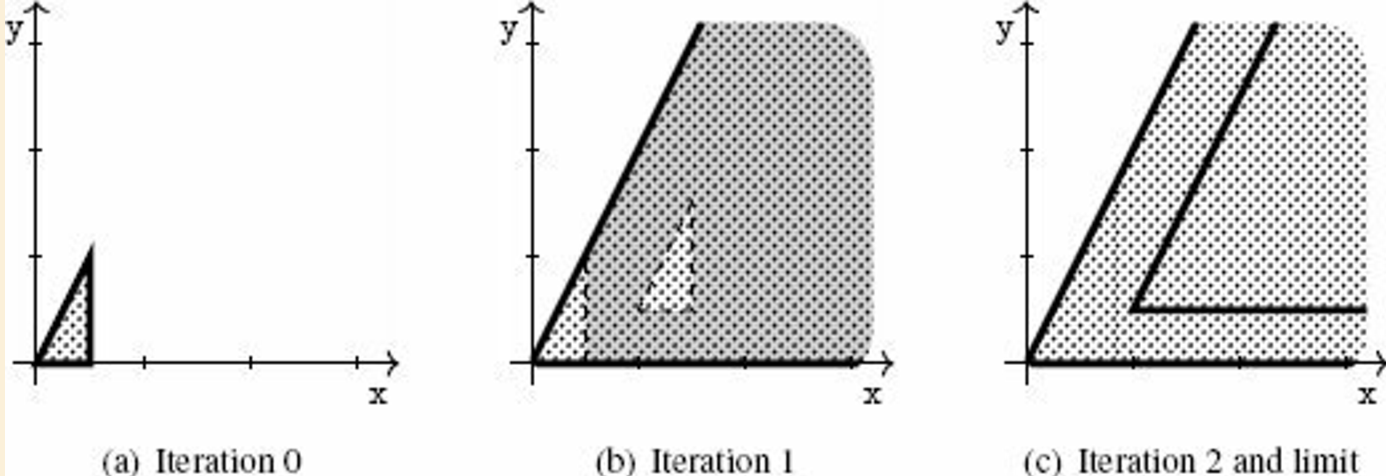
2.3.4 Abstraction of Non-Deterministic Iteration
setup:
program
pconsists of a loop with bodyb:piter{ b }: program that iterates
btimes: program that iterates
bat most timesimplies: is equivalent to or
idea: recursively applies analysis
analysis converges if
Rstabilizes
approach: force the number of abstract elements to decrease over iteration
widening: over-approximatesunions, enforces convergence:
keeps all constraints of that are also satisfied in and
discards all constraints of that are not satisfied in (hence to subsume )
inclusion: inputs abstract elements and returns true only when it can prove that
Algorithm:
R ← a;
repeat
T ← R;
R ← widen(R, analysis(p, R));
until inclusion(R, T)
return T;Widening is another source of potential incompleteness, but fortunately there are many techniques to make the analysis of loops more precise.
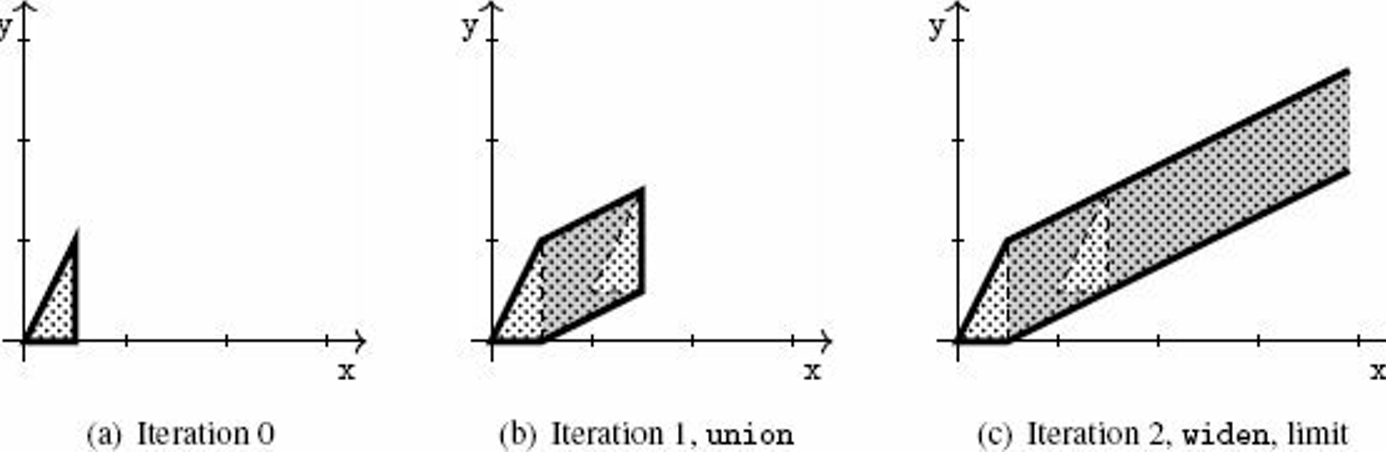
To unroll the first iteration of the loop into the union of {{}; b} can ease the effect of the succeeding widenings.
program that acts on 2D space | abstract iteration | |
|---|---|---|
original | |
|
loop unrolled | |
|
2.3.5 Verification of the Property of Interest
The analysis discussed so far actually computes as intermediate results over-approximations for all the interesting states of the input program, and thus we can just monitor them and use it for the verification of the property of interest.
2.4 A Computable Abstract Semantics: Transitional Style
Idea: compute, from the outset, all occurring intermediate states
2.4.1 Semantics as State Transitions
The goal of the analysis: to collect all the states occurring in all possible transition sequences of the input program.
program: a collection of statements with a well defined execution order
program counter (program point): a unique label assigned to each statement of the program
control flow: the execution order, specified by a relation between the labels (from current program points to next program points)
The algorithm works very similarly to the "compositional style", but it will compute states per statement and iterates until all the statement states get converged.
2.5 Core Principles of a Static Analysis
The three-stage approach for static analysis:
selection of the semantics and properties of interest
choice of the abstraction
derivation of the analysis algorithms from the semantics and from the abstraction
Last modified: 2023-02-16.
Website built with Franklin.jl and the Julia programming language.